Department of Image Processing

Translation, rotation, and scaling (TRS) are the simplest transformations of spatial coordinates. TRS, sometimes called similarity transform can be described as

where (a_0,b₀)^T is a translation vector, s is a positive uniform scaling factor and α is the angle of rotation. Complex moments are suitable for creating TRS invariants. The normalized central complex moment of order (p+q) of the image f is defined

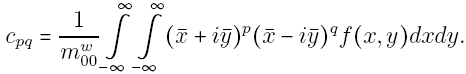
x=x-x_t and y=y-y_t are coordinates translated so the centroid (x_t,y_t) of the image is in the origin of the coordinates, w=(p+q)/2+1 provides correct normalization to scaling, i is imaginary unit, and x_t=m₁₀/m₀₀ and y_t=m₀₁/m_00. m₀₀, m₁₀, m₀₁ are geometric moments

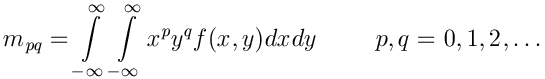
The TRS invariants are then constructed

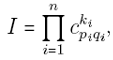
where

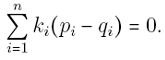
We should use only complete and independent sets of invariants, creating so called basis. Special attention must be paid to recognition of symmetric object, where many complex moments are zero.

To illustrate it, we carried out a following experiment. We used a popular baby toy that is also commonly used in testing computer vision algorithms and robotic systems. The toy consists of a hollow sphere with twelve holes and of twelve objects of various shapes. Each object matches with one particular hole. The baby (or the algorithm) is supposed to assign the objects to the corresponding holes and insert them into the sphere. The baby can employ both the color and shape information, however, in our experiment we completely disregarded the colors to make the task more difficult. First, we binarized the pictures of the holes (one picture per each hole) by simple thresholding. Binarization was the only pre-processing, no sphere-to-plane corrections were applied.

Since all objects have some type of symmetry, we did not use the invariants of low orders that would be zero or almost zero, we used the following three invariants: c₆₀c₀₆, c₅₀c₀₅, and c₄₀c₀₄ instead. They were used as features of minimum-distance classifier. We took weighted Euclidean distance, where the weights were set up to normalize the dynamic range of the invariants. The invariants of the holes were used as representatives of the classes. Then we took five pictures of each object with random rotations, binarized them, and run the classification. This task is not so easy as it might appear because the holes are a bit larger than the objects but this relation is morphological rather than linear and does not preserve the shapes exactly. Fortunately, all 60 unknown objects were recognized correctly and assigned to proper holes.

The toy set and the feature space can be seen on the following figures.

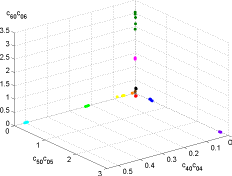Contact person: Jan Flusser , Tomáš Suk

Publications:

1. Flusser Jan, Suk Tomáš, Zitová Barbara: Moments and Moment Invariants in Pattern Recognition, Wiley & Sons Ltd., 2009.
2. Flusser Jan, Suk Tomáš: Rotation Moment Invariants for Recognition of Symmetric Objects, IEEE Transactions on Image Processing vol.15, 12 (2006), p. 3784-3790, Download PDF
3. Flusser Jan, Suk Tomáš: Construction of complete and independent systems of rotation moment invariants, Computer Analysis of Images and Patterns. Proceedings, p. 41-48, Eds: Petkov N., Westenberg M. A., Springer, (Berlin 2003), International Conference CAIP 2003 /10./, (Groningen, NL, 25.08.2003-27.08.2003), Download PDF
4. Flusser Jan: On the inverse problem of rotation moment invariants, Pattern Recognition vol.35, 12 (2002), p. 3015-3017, Download PDF
5. Flusser Jan: On the independence of rotation moment invariants, Pattern Recognition vol.33, 9 (2000), p. 1405-1410, Download PDF

Relevant publications by other authors:

1. C. H. Teh and R. T. Chin, “On image analysis by the method of moments,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 10, no. 4, pp.
   496–513, Apr. 1988.
2. M. R. Teague, “Image analysis via the general theory of moments,” J. Opt. Soc. Amer., vol. 70, pp. 920–930, 1980.
3. M. K. Hu, “Visual pattern recognition by moment invariants,” IRE Trans. Inf. Theory, vol. 8, pp. 179–187, 1962.