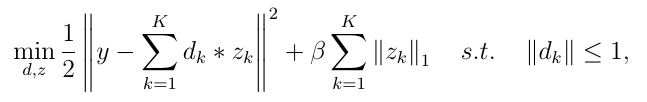Fast convolutional sparse coding using matrix inversion lemma
This web page describes results published in our paper: Michal Šorel, Filip Šroubek, Fast convolutional sparse coding using matrix inversion lemma, Digital Signal Processing, vol. 55, pp.44-51, 2016.
Convolutional sparse coding is an alternative to standard sparse coding better suited for modelling shift-invariant signals. The most time-consuming part of both kernel learning and feature extraction is inversion of certain linear operator related to convolution. In this work we show how these inversions can be computed non-iteratively in the Fourier domain using the matrix inversion lemma even for multiple training signals. This greatly speeds up computation and makes convolutional sparse coding computationally feasible even for large problems.
The matrix inversion lemma to speed up the convolutional sparse coding was already independently used in recent papers B. Wohlberg, "Efficient Convolutional Sparse Coding", 2014, F. Heide, W. Heidrich, G. Wetzstein, "Fast and flexible convolutional sparse coding", 2015 and B. Wohlberg, "Efficient Algorithms for Convolutional Sparse Representations", 2016. The main problem of these methods is that they work efficiently only with one input image. In practice we would like the kernels to represent well not one particular signal/image but a larger set of examples. Our main contribution is that the proposed method is fast even for such cases.
Matlab code implementing several variants of the proposed algorithm and our implementation of other methods (Zeiler et al. 2010, Bristow et al. 2013, Wohlberg 2016) is available on GitHub.
The convolution sparse coding problem is formulated as a minimization task:
|
|
(1) |
where y is the observed signal (image or a set of images), zk are sparse features and dk are convolution kernels. Both zk and dk are unknown and must be estimated while forcing feature sparsity (the second L1-norm term) and limiting the energy of kernels (inequality constraint). In other words, we are looking for a set of convolution kernels and corresponding sparse feature maps such that their convolution and summation generates the observed signal.
In practice, the convolution sparse coding runs in two phases: kernel learning and then feature extraction. Given the observed set of signals we first have to learn the convolution kernels d. We solve the above problem (1) with respect to d and z, but keep only d for later use. In the second stage, the learned kernels are used for feature extraction. A new observation arrives and we need to calculate features for classification. This is done by solving the above problem (1) with respect to the feature map z only, since convolution kernels are known from the learning phase.
If (1) is formulated for multiple images yl's (sum over l is added in front of the first term), then the matrix inversion lemma cannot be applied directly. We propose three different remedies. One is "tiling", which means that one large "patchwork" y is created from all yl's. Second one is "3D composition", which means that yl's are stacked along the third dimension (in general N+1 for signals of dimension N). Both approaches require a relatively large memory overhead to keep all auxiliary variables. The third remedy alleviates the memory overhead by reformulating convolution sparse coding as a global consensus problem, which divides the problem into smaller sub-problems that can be solved sequentially on a device with limited memory or in parallel on several such devices.
The following figure shows an example of kernel learning from 50 images of urban scenes. Three sets of kernels with different size were learned simultaneously: 8x8, 32x32 and 64x64. Kernels are sorted by energy of the corresponding feature map in a descending order from top-left to bottom-right. We can observe that the high energy kernels contain meaningful structures whereas the low energy are more noisy.
 |
| 8 kernels of size 8x8 |
 |
| 32 kernels of size16x16 |
 |
| 64 kernels of size 32x32 |
| Details: | |
| Duration: | 2014-2015 |
| Contact person: | Michal Sorel |
| Involved people: | Filip Sroubek |
Publications: